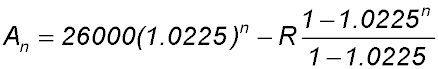Finance - Series - Loans TYS 1

The questions on this page focus on:

2. Increasing the regular repayment amount.

Strategy: When approaching questions involving changes to rates, deposits or making special deposits, it is usually a good strategy to sove the expression you develop for the last period before the change. Then carry the amount you calculate into the next phase rather than try to extend the series pattern. Less writing and less chance of errors

Changing the interest rate.	1. It is a common practice to provide loans at a special "introductory rate" for some time and then revert to a "normal" rate. Phoebe was offered such an incentive when she borrowed $150,000 on a 15 year monthly reducible loan to buy her first apartment. The introductory rate was 4% for two years rising to the usual 6% after 24 months. She felt she could afford $1,500 per month for repayments during the initial period. (i) How much did Phoebe still owe on her loan at the end of 2 years? (ii) What was Phoebe's monthly repayment amount for the remainder of her loan? (iii) If Phoebe maintained her monthly repayment at $1,500, when would she have repaid her loan in full? Answer.(i) $124,942.11 owing at end Y2. (ii) $1,361.47 p.m. (iii) Loan ends 24 months earlier.
	2. One year ago, Harry and Sally borrowed $350,000 to purchase a house. The terms of the loan were a 25 year period with 9% monthly reducible interest rate. The monthly installments were set at $2,937. (i) Show that Harry and Sally owed $346,098 (to the nearest dollar) at the end of the first year. (ii) At the end of the first year, their interest rate was reduced to 6% p.a. monthly reducible. What is their new rate of monthly repayment if the loan is to be paid off over the agreed 25 year period? (iii) If Harry and Sally maintained their original repayment level of $2,937, how much sooner would they be clear of their loan commitment? (iv) How much will they save? Answer.(i) $346,095 owing at end Y1. (ii) $2,270.31 p.m. (iii) Loan ends after 15 years - so 10 years early!! (iv) Saving of $128,126.
	3. A loan for $L was taken out by a small business just starting up its operations. The conditions of the loan were: interest was to be charged at 6% p.a. for the first three months; repayments would be made in equal monthly installments of $4,000 over the three year life of the loan; the interest was to be charged monthly before each repayment. If $A_n is the amount of the loan still owing after the nth repayment: (i) Find an expression for A₂. At the end of the three months initial period, the interest rate was increased to 9% p.a. and that rate was to be maintained for the remainder of the loan. The loan was then to be repaid in equal monthly repayments of $4,800 for the remainder of the three year period. (ii) Find an expression for A₄ (iii) Find the amount of the loan $L (to the nearest $100). Answer.(iii) Loan of $149,700.
	4.
	5.
Increasing the regular repayment amount.	6. Pete borrows $150,000 from his bank and agrees to repay the loan in equal monthly installments of $1,075 at the end of each month over 20 years. The interest rate is 6% p.a. (i) Calculate the amount he owes on the first day of the third month. (ii) If $A_n is the amount he owes at the end of n months, show that $A_n = $215,000 - $65,000 × 1.005ⁿ (iii) At the end of the 5^th year (and after the monthly repayment has been made) Pete decides to increase his monthly repayment to $1,500 (without penalty). How many years and months will Pete save in paying off the loan. (iv) How much will the change save him in interest payments? Answer.(i) $149,348.38. (iii) 9 years 3 months. (iv)
	7. Ben borrows $200,000 from a bank. He wants to make payments of $P at the end of each month over 25 years. The bank offers him interest at 6% p.a. monthly reducible. If $B_n is the balance of the loan after n months: (i) Show that B₃ = $200,000 × 1.005³ - P(1 + 1.005 + 1.005²) (ii) By generalising that equation and setting it equal to zero balance after 300 months, find Ben's monthly repayment amount $P. (iii) After 10 years,(and the 120th repayment) Ben feels he can afford to increase his repayment amount to $2,500. If he maintains his original interest rate, how many more years is it before Ben pays off his loan? Answer.(ii) $1,288.60 monthly. (iii) 7 years 1 months + $175.
	8. Paulina charged $5000 on her credit card at the beginning of January 2019. Her debt was to be repaid by equal monthly installments of $100. The first installment was due on 1 February. Interest rate on the credit card is 18% p.a. calculated at the beginning of each month on the balance at the end of the previous month. The interest is added to the outstanding amount before the monthly repayment installment is paid. (i) Show that the amount Paulina owes on her credit card after her first repayment has been made is $4,975. (ii) If Paulina maintains her repayment schedule, when will she have paid off her debt? (iii) At the end of 2020 (i.e. after 24 months), Paulina plans to have the debt cleared by the end of 2021. How much will Paulina's new monthly repayment be? (iv) How much will Paulina save by her changed repayment strategy? Answer.(i) 93.11 months = 7 years 10 months. (iii) $392.77 p.m. (iv) Saving = $2,197.76!!!
	9. Ellen borrowed $600,000 for the purchase of her home. The interest rate charged was 3.6% fixed over the 30 year term of the loan. Let $A be the amount owing at the end of n months and $M be the monthly payment amount. (i) Show that . (ii) Show that the monthly repayments will be $2,728 (to the nearest $) if Ellen is to repay the loan at the end of 30 years. (iii) Show that Ellen still owes $274,513 after 20 years. (iv) At the end of 20 years, Ellen decides to increase her repayment amount by 0.1% per month so that she can reduce the term of the loan. Show that M₂₄₃ = 27451×1.003³ - 2728 × 1.001(1.003² + 1.003 × 1.001+ 1.001²) (v) By factorising out a "common factor" of 1.003³ from the bracketed term, write the second part of this expression as a geometric series. (vi) Hence calculate the balance of Ellen's loan after 243 months.
	10. Ted wishes to borrow $10,000 from his Bank. The bank sets the conditions that his rate is 6% monthly reducible interest and the repayment period is 24 months. (i) Show that the amount owing after the first two months can be expressed as . (ii) Calculate the monthly repayment $R and so calculate the amount of interest Ted pays on this loan over the two years? (iii) Ted proposes to the Bank that he wants to start with lower monthly repayments and work up as his income increases. His suggestion is to start with an amount $D in the first month and increase that deposit by 1% every month. Calculate the amounts Ted pays in each of the first three months. (iv) Hence calculate the total amount Ted pays in interest over the 24 months. (v) Explain the differences in the interest amounts between these two repayment strategies especially in terms of the amounts being paid each month. Answer.(ii) $443.21 monthly so a total of $10,637.04. (iii) First 3 months are $395.29, $399.24, $403.24. (iv) Total = $10,662.34.
Making a special contribution.	11. Jonah borrowed $26,000 at 9% monthly reducible interest. He intends to repay the loan in quarterly repayments of $R over two years. If A_n is the amount outstanding on the loan immediately after the n^th payment: (i) show that (ii) Show that the value of each repayment is $3,387.60. (iii) When Jonah made his 4th repayment, he immediately paid an additional $2,000. Determine the amount by which his final repayment will be reduced as a result of the additional payment. Answer.(iii) Final payment is reduced by $2,185.66. (iii) First 3 months are $395.29, $399.24, $403.24. (iv) Total = $10,662.34.
	12.
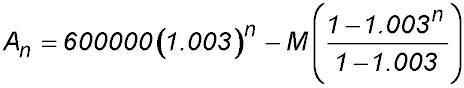